New to me, thanks @hpschdNU, what are my learned colleagues thoughts on this?
According to Baroque musicians, once all the fifths are playable, the most important matter in a circular temperament is the size of the 12 Major Thirds, which, ordered by the sequence of fifths (C-E, G-B, D-F# and so on) is called “Circle of Major Thirds”. I fail to see this information in this page about the Jagermeister/Haugsand tuning. It is utterly confusing in that, contrary to the present use by about 99% of temperament scholars, does not use the Cent but the TU (temperament unit) and further confuses the matter by making reasonings in Hertz. Being conversant with the matter, I gave a cursory reading and found these charts very difficult to understand. They do not give me what I need to know: how deviated are the 12 major thirds in Cents? How does this compare to other temperaments?
This “explanatory” webpage is supposed to explain the TU and equivalences to other units, but instead of relating it to the Cent, it relates it to Pythagorean comma fractions.
In my U.T. Book I have explained why scholars do not use the TU: it provides nice numbers provided you move within German Good temperaments (and not even all of them!) that temper fifths by “nice” fractions of the Pythagorean Comma. For many other temperaments, the TU is utterly confusing.
The webpage relates the TU to the Pyth. Comma, providing exact ratios, and also to the Syntonic Comma, providing only APPROXIMATIVE ratios!
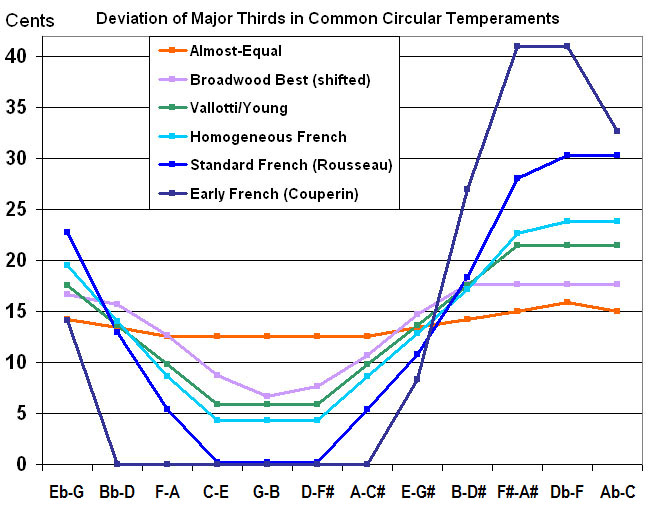
In my U.T. I provide a single major thirds curve for a temperament, and a comparison curve to another temperament, all you need to know, in a small chart, no calculations, no curves that show deviation based on whether they are horizontal or else. I enclose, for example, my general curve of comparison of main baroque circular temperaments: within a single simple chart, all you really need to know about SIX temperaments!
Of course, to understand the sizes of the Major Thirds in Jägermeister, I could take the sizes of the major thirds in TU from the webpage of Mr Tungland and convert them to Cents, but these basic numbers are not there! Not even the fifth sizes for the Circle of Fifths are there! I start reading reasonings based on beats, which are useful only for modern tuning methods, but fail to be useful to scrutinise the size of intervals. ![]()
There are MANY more shortcomings in Mr Tungland webpage. There is no historical explanation of how Jägermeister relates to historical Baroque practice! Why should I use it? How different is it from Equal Temperament, or from Werckmeister III? Why use new and confusing concepts to explain very simple things with simple mathematical tools that have been in universal use ever since Ellis, almost 150 years ago? ![]()
I googled and found Ketil’s own explanation in Facebook.
"GROUP ONE: all the fifths and fourths between c#’ and f’:
- c#’ - g’#: pure, or a smidgeon wide (!)
- f’ - b-flat’: pure, or a smidgeon narrow (!)
- e-flat’ to be set “between” g#’ and b-flat’ - “almost pure” to both
- don’t forget to tune b-flat to b-flat’ (!)
- This group i the irregular group - with its wide 5ths and narrow 4ths! The next two groups are regular, with narrow 5ths and wide fourths.
GROUP TWO: All the 5ths and 4ths between f’ and a’: - Tune these 5ths NARROW, ca. 2 b.p.s. and the 4ths WIDE, ca. 2b.p.s., “matching” them to each other, creating a similar ring to all of them on comparison.
GROUP THREE: The remaining 5ths and 4ths, a’ to c#’ - same procedure as above, but a slightly purer tempering than these. - Don’t change the control notes, once they have been set!
- Don’t give up right away!
- If C major and the other central keys, F, G, D sound outrageous, you’ve done something wrong, like a wide fifth somewhere in group 2 or 3…"
This is just an empirical tuning method, hardly based on Baroque practice, and further very approximative and difficult to reduce to numbers.
No doubt the result is fine for tuning practice, but it does not tell me how the final result will be compared to well-known historical circular temperaments.
Will keep googling to see whether I can have the size of the 12 fifths in Jägermeister: any unit (even the TU) will do for this purpose …
In the same Facebook exchange Bradley Lehman intervenes. But he does NOT calculate the numbers for Jägermeister. He just shows that, tweaking it a little bit, it becomes … Lehman’s own Bach temperament. We already knew this, didn’t we? And I keep searching …
In the several Tungland pages I see, advertised as a good things, expressions such as “more than 175 tunings!”. Supposedly, the harpsichordist wishing to tune his instrument in order to play Baroque music asking for circular temperaments, should try hundreds of tunings and then select one (which, in this confusion, will surely be a poor choice).
Why not do it the historical way? Find out the handful of circular temperaments that have either a historical or an acoustical basis for our purpose, scrutinise them with Major Thirds deviations, and then decide? Isn’t it hundred-fold easier?
Tungland appears to be a follower of Lehman who, against all the plenty and very clear historical record (whereby “a temperament is judged by the thirds”), prefers instead to use convolute reasonings based on vibrations, beats, sizes of tones and semitones …
Oy, Claudio,
How to even BEGIN to react to your many messages “rant”. I think it only need be said that Ketil’s explanation of his temperament actually sounds a lot more like contemporary Baroque descriptions of historical temperaments. And historical temperaments DIDN’T rely on numbers (to a 10th of a cent) or needles on a machine or in an app. I think it also fair to say that, though we rely on our machines and temperaments, people like Paul Poletti have always been up front that when they list numbers for a historical temperament, it is an interpretation and subjective. I think it is also fair to say that, before the advent of tuning machines and apps, the way a real tuner tuned an instrument might differ from the way another tuner would tune the same temperament using the same description. This, of course, explains why “equal temperament,” even in the early 20th century, wasn’t quite yet perfect equal temperament, at least as far as mathematics, machines, and apps were concerned. The goal of temperaments is to compromise and satisfy the need to tune a 12 note per octave keyboard instrument in a way that sounds good, is useful in whatever keys are needed in a particular situation, and be playable with an ensemble of real instruments, players, and singers. Ultimately, it is the musical result that is important, and everything else is just NOISE!
Dongsok
Have you read Werckmeister, Dongsok? He was the best read German Baroque source on temperaments. And he DID use numbers to define his temperaments. Neidhardt did also.
I do not understand your comment on Poletti: I agree with his ways.
As for your second sentence, I have explained this matter many times, also in publications, well, here it goes again!: Numbers are needed to deduce and understand the properties of temperaments, and to judge their adequacy to this or that historical source or musical score. You cannot understand the musical result of a temperament without numbers: this is what amateurish work peddles sometimes, and has been debunked by many scholars.
On the other hand, and I have also repeated this ad nauseam, nobody has ever said that mathematics are needed in everyday’s tuning and musical practice.
By the way, Dongsok, you should appreciate my own ways, reducing the mathematics of a temperament to a single curve, easy to appreciate on a chart without reading a single number, as I have shown above.
Compare such a chart with the hundreds of numbers, in different units, shown in Tungland’s webpage!
Aren’t you barking at the wrong tree?
I do appreciate the quality of your graphics as opposed to the Tungland’s numbers. And of course I appreciate your book on temperaments which I often refer to when I need, even though I confess I skip the mathematics parts because they are too difficult/tiring for me and because I am not too much interested in the subtle details of tuning. Fortunately math is not necessary in everyday practice, as you say.
But isn’t mathematics only a way (maybe the only serious way) to describe or analize the temperaments outside the musical environment? I would think you can “understand the musical results of a temperament” without numbers, just by tuning and playing/hearing. But probably I am missing something again.
Indeed, probably the baroque harpsichordists weren’t so precise when tuning. After all, they weren’t even counting beats but only judging intervals quality and “colour”, so I guess a certain fuzzyness was in order. Isn’t it something we often do even today in our daily practice, when tuning by ear? At least, I certainly do hope so, I am sure I could never reach the degree of precision of an electronic tuner (nor I feel the necessity). I think I’m not alone, as I see colleagues, teachers, concertists, tune in a approximate way, say a “Rameau-ish” temperament, a Neidhard-ish temperament and so on (meantone is always set precisely, though).
Finally, I confess I had ever believed the “Jägermeister temperament” was a joke by Ketil Haugsand, he loves joking. I didn’t even suspect it was a real thing, shame on me. ![]()
My first resolutions for 2023 (as well as starting again to play tennis): learn the Bach/Barnes temperament and use when learning to play the Goldbergs.
Claudio, do you think Bach/Barnes is good for Scarlatti? I’d like to stick with two temperaments only, meantone and a circular one, so I can do without apps and electronic tuners.
Please read my U.T. book, p.181, about work on D. Scarlatti’s temperament. In a word: use Vallotti! ![]()
(Which anyway is Barnes but for a small difference in the note B)
And yes, of course mathematics is only a way to analyse outside the music making. But the conclusions of mathematics give you direct answers for specific music. Baroque musicians spent years before reaching, for music composed in a restricted place and time, a decision on temperament. We play on the harpsichord music composed across centuries all over Europe, with different temperaments. Just by experimenting, like Baroque musicians did, a lifetime would not be sufficient! We need historical and mathematical work to reach a conclusion before we start tuning! Otherwise, we will tune unhistorically. And only 1 out of 100 in the audience will note the difference!
Vallotti has been mentioned more than once. Another day and in another “category” I will discuss Vallotti: why it was used for decades until recently, especially after it was shown that it was ideal for J.S. Bach. And why it is fully historical and musically most fitting for late Baroque music, while Neidhardt’s circular temperaments are not. The explanation is highly complex, and is dealt with in many pages of my U.T. Book. For just a sample, the following paper can be freely downloaded online: Vallotti as the ideal German Good Temperament
I did read it, of course! I’ve used Vallotti for many years. I just grew a bit tired of it and wanted to try something new. The real truth however is I never managed to learn Vallotti by ear, shame on me. I have nothing against electronics, in fact I love them. But I don’t want to be dependent on electronics which may fail.
New resolution for 2023: learn Vallotti by ear.
Dom
Ps I’m going to re-read your book, this discussion arose many questions in my mind but I don’t want to ask before re-reading.
Here is the video explaining it from the ‘author’ himself
The instructions quoted above from FB don’t mention the crucial initial step of setting the major thirds f’-a’ and a-c#’ to have the degree of impurity you want … which then gives you the ‘middle’ third c#‘-f’ as the remainder of the octave.
The recipe works very well if you start from a fixed A and you want the ‘worst’ intonation to be around C#/Db major or Bb minor and the ‘best’ around F major.
The caricature of this in terms of ‘Neidhardt units’ (1/12 Pythagorean comma) is as follows
C -2 G -2 D -2 A -1. E -1. B -1. F# -1. C# 0~ G# 0+ Eb 0+ Bb 0~ F -2 C
where ‘-1.’ means a bit more than 1/12 comma and ‘0+/0~’ mean ‘nearly pure, whatever’. It is not far from Vallotti ![]() but slightly kinder to the sharp side, A major may be a bit better than ET.
but slightly kinder to the sharp side, A major may be a bit better than ET.
If you want something slightly different, you can start from this point and (say) lower F slightly and lower E and B slightly and tweak the sharps a bit or whatever. You could end up with eg
C -2 G -2 D -2 A -2 E -1 B -1 F# -1 C# 0~ G# 0~ Eb 0~ Bb 0~ F -1 C
This is definitely preferable to Vallotti for a ‘typical’ range of later Baroque tonality favouring sharp side for consonance vs flat side for ‘suffering’.